What is a Stream Graph?¶
A stream-graph is a generalization of a static graph. As we know a static graph, is an object \(G = (V, E)\), where:
\(V\), is a set of nodes or the node-set
\(E \subseteq V \times V\), is a set of links or the link-set
A stream-graph, is an object \(S = (V, T, W, Z)\), where:
\(V\), a set of nodes or the node-set
\(T\), a collection of time-objects or the time-set
\(W \subseteq V \times T\), a collection of temporal-nodes or the temporal-node-set
\(Z \subseteq (W \times W) \; / \; T \subseteq V \times V \times T\), a collection of temporal-links or the temporal-link-set
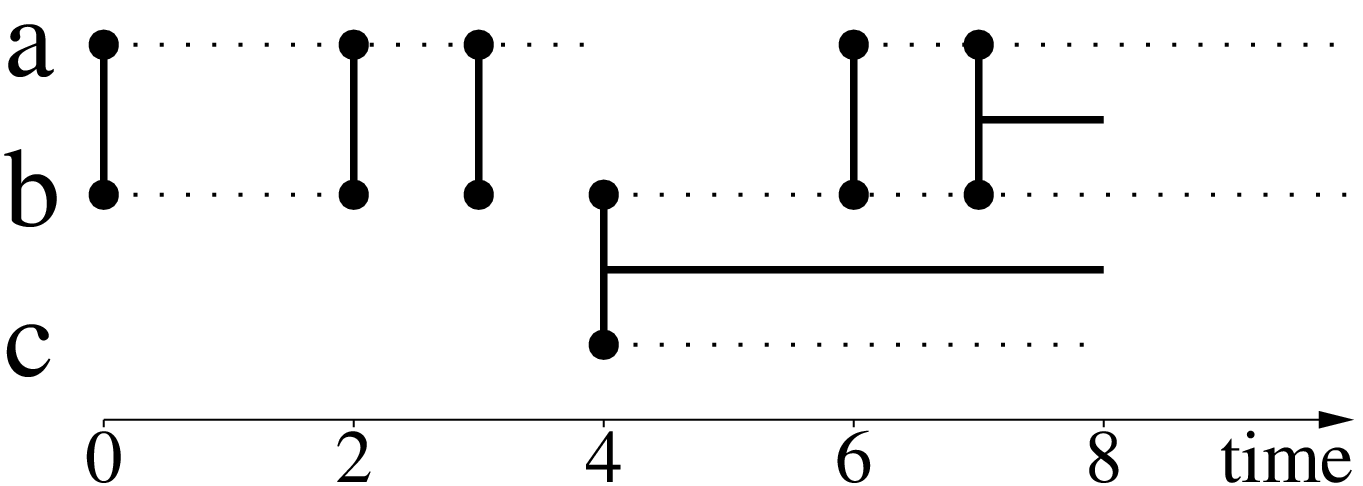
Notice that in a stream-graph we can have both instantaneous and interactions with duration.
Additionally it is important to define a time-signature. Distinction between discrete and continuous time makes a difference on applying operations between temporal-obejects. All the differences arise from the fact that only for discrete-time, all interactions with duration, can be represented as instantaneous interactions and vice-versa.
We will refer to the aggregated graph \(G_{S} = (V, E_{Z})\) of a stream-graph as the one defined by it’s nodeset \(V\), and it’s induced link-set \(E_{Z} = {(u, v) | (u, v, _) \in E}\) of all the links that appear inside the temporal-link-set.